4. オイラー関数

　このオイラー関数は，1760年にオイラーがフェルマーの小定理を素数でない場合に拡張することを目的に．自然数$n$について，$n$以下で$n$と互いに素である数の個数と定義したものです。
　一方で，行列(matrix)や3次方程式以上の判別式(discriminant)という用語を産みだし，米国初の数学雑誌・American Journal of Mathematicsを創刊したことでも知られるシルヴェスターが呼称したオイラーのトーシェント(totient)関数とも呼ばれることもあります。これは1879年にシルヴェスター(J. J. Sylvester, 1814-1897)が自然数$n$についての"totitive"($n$以下でその数と互いに素な数)の概念を導入(Sylvester, On Certain Ternary Cubic-Form Equations, American Journal of Math., Dec., 1879, Vol.2, No.4 (Dec.,1879), pp. 357-393; p.378に記述)し，この個数を $n$ の "totient" と呼び $\varphi(n)$ を $\tau(n)$ として利用したことから生まれた呼称となります(Sylvester, On Certain Ternary Cubic-Form Equations, American Journal of Math., Dec., 1879, Vol.2, No.4 (Dec.,1879), pp. 357-393; p.361 に記述，L.E. Dickson, History of the THEORY OF NUMBERS Vol.1, p.124 (1919). でも追述 )．初等整数論を少しでも学んだことのある人にはお馴染みかもしれません。
　

　1760年当時，オイラーは自然数$n$について，$n$以下で$n$と互いに素である個数を$\pi\ n$と表記し，現在のオイラー関数といわれるものを定義しました。このときは${\mathbf\pi}\ 1=0$としていました。(L. Euler, Leonhard, Speculationes circa quasdam insignes proprietates numerorum, (1784). Euler Archive - All Works. 564. ; L. Euler, Acta Ac. Petrop.,4 II (or 8), vol.1780 (1775), 18; Comm. Arith., 2, 127-133.)
　因みに，藤原松三郎(1881-1946)によれば，江戸時代の和算家・久留島義太(くるしま よしひろ, ?-1757)がオイラーよりも前に発見していたといわれています．(藤原松三郎，(川原秀城解説)，日本数学史要，(1952年宝文館発刊，復刻版)，勉誠出版，2007)

　現在の$\varphi(n)$の表記は，後にガウスが"Disquisitiones Arithmeticae"(1801)の中で表記し，オイラーの$\mathbf\pi\ 1=0$を避け，便宜上$\varphi(1)=1$と定めたものです。つまり，

　 $$ \begin{align*} \varphi(n)=\left\{ \begin{array}{ll} \displaystyle \sum_{\substack{1\leqq k\leqq n\\ (n,k)=1}}1 & (n>1) \\ \qquad 1 & (n=1) \end{array} \right. \end{align*} $$

　4.1. フェルマーの小定理

フェルマーの小定理

　素数$p$に対して，$(a,p)=1$である整数$a$について，次が成立する．
　$a^{p-1}\equiv 1 \pmod{p}$ 　　

　　証明してみましょう．これについては，いくつかの証明が知られています．
　$a^p\equiv a \pmod{p}$ を示すことができれば，$(a,p)=1$を用いて，合同式の基本性質より $a^{p-1}\equiv 1 \pmod{p}$ を導くことができるので，目標を　すべての$a$ について$$ \begin{align*} a^{p}\equiv a \pmod{p} \end{align*} $$ が成立するとしてよいことが分かります。
　$a=1$のときは，$a^p=1^p=1=a$ であるので成立しています．
　$a=k$のとき $$ \begin{align*} k^{p}\equiv k \pmod{p} \tag{*f1} \end{align*} $$ 　が成立しているとすると
　$a=k+1$のとき，合同式の性質から $$ \begin{align*} (k+1)^{p}\equiv k^p+1^p\equiv k+1 \pmod{p} \end{align*} $$ 　よって，帰納法から示されます．

　4.2. オイラー関数とは

　

　4.4. オイラー関数の諸性質

オイラー関数の諸性質

• 正の整数$n$について$\varphi(n)\lt n$．
• 正の偶数$n=2^en'\quad (2,n')=1$ について$\varphi(n)=$．
• オイラー関数は乗法的である．すなわち $(m,n)=1$である正の整数$m,~n$については $$ \begin{align*} \varphi(mn)=\varphi(m)\varphi(n) \end{align*} $$

　3番目については，次のように見てみましょう．
　　$1,~a_{2},\cdots,a_{\varphi(m)}$ を，$m$以下の$m$と互いに素な$\varphi(m)$個の整数とします．このとき， $$ \begin{array}{rrcr} 1 & a_{2} & \cdots & a_{\varphi(m)} \\ m+1 & m+a_{2} & \cdots & m+a_{\varphi(m)} \\ 2m+1 & 2m+a_{2} & \cdots & 2m+a_{\varphi(m)} \\ \cdots & \cdots & \cdots & \cdots \\ (n-1)m+1 & (n-1)m+a_{2} & \cdots & (n-1)m+a_{\varphi(m)} \end{array} $$ 　は，$mn$以下の$m$と互いに素な自然数を1行目 $1,~a_1,~a_2,\cdots,~a_{\varphi(m)}$ から$n$行目まで$\varphi(m)$個づつ並べた表です．この中に$mn$と互いに素な自然数がいくつあるかを調べましょう．
　次に，この表を各列ごとに見てゆきます．例えば，1列目の $1,~m+1,~2m+1,~(n-1)m+1$ の$n$個の中に $\mod n$ で$n$と互いに素である自然数が$\varphi(n)$個あります．というのは，$(m,n)=1$から，$im+1\not\equiv jm+1,\quad 0\leqq i\ne j\leqq n-1$ がわかり，1列目の$n$個の自然数は$\mod n$で互いに異なることから，この中に$n$と互いに素である自然数は$\varphi(n)$個あります．同様に各列に$\varphi(n)$個あり，列数は$\varphi(m)$なので，これらで$mn$と互いに素である自然数はすべて尽くされているので，$\varphi(m)\varphi(n)$個であることがわかり，$\varphi(mn)=\varphi(m)\varphi(n)$を得られます．$\square$

　4.5. オイラー関数を繰り返してみる

　・・・・・
　オイラー関数 $\varphi$ では$n>1$について$\varphi(n)\lt n$が成り立っていることから， $$ \begin{align*} \varphi(\varphi(n)),~\varphi(\varphi(\varphi(n))),\cdots ,~\varphi(\varphi(\cdots (\varphi(n))\cdots )) \end{align*} $$ とオイラー関数を繰り返して作用させてゆくと，いつかは$1$にたどり着くことがわかります．
つまり，$\varphi^{k}(n)=\varphi(\varphi^{k-1}(n)),(k\geqq 2),\quad \varphi^{1}(n)=\varphi(n)$と書くことにすれば，どのような$n$についても，ある($n$に依存する)$k=k(n)$で初めて$\varphi^{k}(n)=1$となることがわかります． $$ \begin{align*} \varphi(2)&=1 \\ \varphi(3)&=2,~\varphi(2)=1 \qquad \varphi(\varphi(3))=\varphi^2(3)=1 \\ \varphi(4)&=2,~\varphi(2)=1 \qquad \varphi(\varphi(4))=\varphi^2(4)=1 \\ \varphi(5)&=4,~\varphi(4)=2,~\varphi(2)=1 \qquad \varphi(\varphi(\varphi(5)))=\varphi^3(5)=1 \\ \varphi(6)&=2,~\varphi(2)=1 \qquad \varphi(\varphi(6))=\varphi^2(6)=1 \\ &\cdots \cdots \\ \varphi(100)&=40,~\varphi(40)=16,~\varphi(16)=8,~...,~\varphi^6(100)=1 \\ &\cdots \cdots \end{align*} $$ という具合です．
　では，何回で$1$にたどり着くのか，その回数$k(n)$を計算してみましょう．

　この$k=k(n)$についての性質をインドの数学者・ヴァイディアナタスワミ(R. Vaidyanathaswami)から提起された問題として初めて調べたのが，インドの数学者ピライ(S. S. Pillai)でした．（S. S. Pillai,ON A FUNCTION CONNECTED WITH $\varphi(n)$, Bull. Amer. Math. Soc. $\bf 35$(1929), 837-841；S. S. Pillai, On an arithmetic function, Annamalai University Journal, ${\bf 2}$, (1933), 242-248）
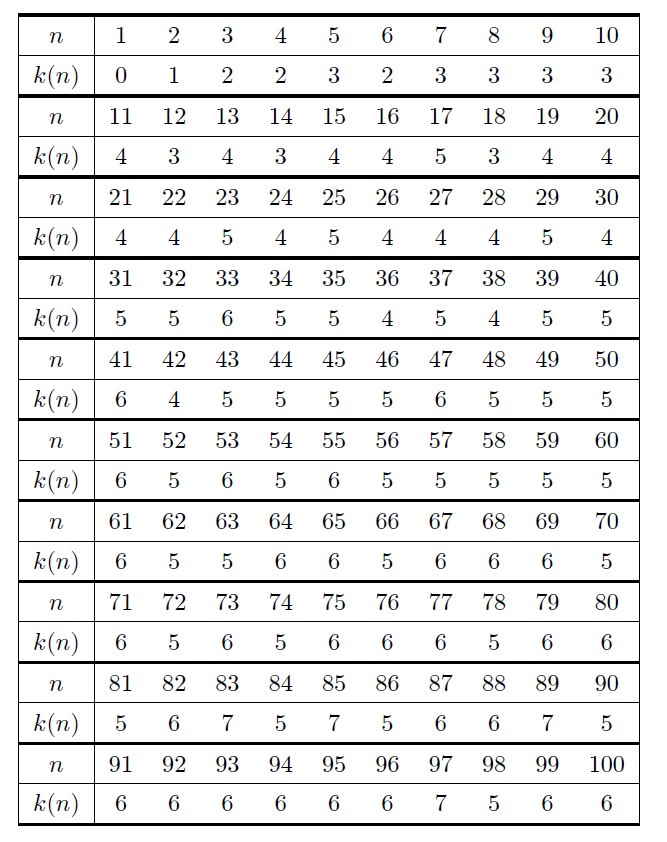
　ピライは$n$についての$k$を$R(n)$として，その簡単な評価式 $$ \begin{align*}\label{PR} \left[ \dfrac{\log n}{\log 2} \right]\geqq R(n)-1\geqq \left[ \dfrac{\log \dfrac{n}{2}}{\log 3} \right] \tag{PR} \end{align*} $$ を導きましたが，以下のような関係式については$n=2^s,~n=2^s\cdot 3^t$の特殊な場合にしか言及できませんでした．
　その14年後，アメリカの数学者シャピロ(H.N.Shapiro，当時Princeton大)が $n$ についての $k$ を$C(n)$, $C(1)=0$とし，自然数 $x,~y$ として，ほぼ対数的な次のような厳密な関係を導き出しました．（H. Shapiro, AN ARITHMETIC FUNCTION ARISING FROM THE $\phi$ FUNCTION, Amer. Math. Monthly ${\bf 50}$ (1943), 18-30）この時点では，シャピロはピライの仕事を知らなかったようです．というのは，このShapiroの論文では，参照文献の記載もなく，Pillaiの結果には触れられていなかったからです． $$ \begin{align*} C(xy)=\left\{ \begin{array}{ll} C(x)+C(y) & (\ x\ \mbox{ もしくは }\ y\ \mbox{ が奇数 }\ ) \\ C(x)+C(y)+1 & (\ x\ \mbox{ と }\ y\ \mbox{ が偶数 }\ ) \end{array} \right. \tag{SC} \end{align*} $$ 　このオイラー関数の繰り返し問題については，シャピロ以降，(シャピロの結果を知らずに結果を得られていたオーストラリアの)バーンズ（E. S. Barnes., Note 225, Australian Math. Teacher ${\bf 11}$ (1955), 20-21）とリンドグレン（H. Lindren, Australian Math. Teacher ${\bf 11}$ (1955), 52-53）以外，実に多くの数学者が様々な形で扱っています．（1960年代では，アラダル（M. Aladar, Az Euler-fél $\phi$ -függvény iterálsával nyert számelméleti függvényröl, Mat. Lapok (Budapest) ${\bf 11}$ (1960), 46-67），パルナミ（J. C. Parnami, On iterates of Euler's $\phi-$function, Amer, Math. Monthly, ${\bf 74}$ (1967), 967-968.）等が知られています）。また，この頃，エルデシュ(P. Erdös)，ポメランス(C. Pomerance)，スッバラオ(M.V. Subbarao)等多くの数論学者が数論的関数のiteration問題を扱っています．
　シャピロが導いた$C(x)$に関する公式は，完全対数的になっていないところが少しばかり残念ではありますが，整数$n$が$\varphi$によって$1$にたどり着く最小回数としては正確に表しているものになります．
　一方，バーンズは$n$に対する最小の$s=s(n)$として$\varphi^s(n)=1$であるとき，$I(1)=0$とした上で $$ \begin{align*} I(n)=\left\{ \begin{array}{ll} s & n\mbox{ が偶数 } \\ s-1 & n\mbox{ が奇数 } \end{array} \right. \end{align*} $$ 　を示し，対数的であることを示しましたが，発表後シャピロの結果を知ったと，先の発表物の中での中で述べていました．
　ここで$L(n)$を次のように決めておくと $$ \begin{align*} L(n)=\left\{ \begin{array}{ll} L(\varphi(n)) +1 & (n \mbox{が偶数のとき}) \\ L(\varphi(n)) & (n \mbox{が奇数のとき}) \end{array} \right. \end{align*} $$ すると，このとき　すべての自然数$x,~y$について $$ \begin{align*} L(xy)=L(x)+L(y) \end{align*} $$ が成立し，$L$が完全対数的(加法的)であることが導かれます．このことは，バーンズやリンドグレンも指摘していました．
　山下が高2のときに気づいた関係式が，この$L$でした．
　大学入学後。様々な初等整数論の成書を開いても，(ボクにとって)面白いこの事実は紹介されていませんでした．また何人かの先生に聞いても反応はなく，M1のときに（B2のときにUBC@ICM1974で面識のあった）内山三郎先生（当時，岡山大）に問うて，初めてこの性質の一連の流れについて知った次第です．修論では扱うことはしませんでしたが．

内山先生からの書簡

　OEIS(A003434)では，$n$が$\varphi$を繰り返すことによって$1$までたどり着く回数として${\bf phiter}$(ココロは phi $+$ iter1ation ?)という数論関数名で扱われています．

　山下は，大学入学時から(当時，秋月－永田の"近代代数学"で導来正規環の学習をしていて，"導来"という言葉を気に入り)勝手にオイラー関数の導来対数関数と呼称していました．
　シャピロは1950年に自身の結果をさらに拡張して（H. Shapiro, On the iterates of certain class of arithmetic functions, Comm. Pure Applied Mth. ${\bf 3}$ (1950), 259-272），$f,\ A$を自然数値をもつ数論的関数で，$f(p_{i})$を素数$p_{i}$については$1\leqq f(p_{i})< p_{i}$，$A$は奇素数$p_{i}$については$A(2)=2,\ 2\lt A(p_{i})\leqq p_{i}$として $$ \begin{align*} f(n)=\prod_{i=1}^{r}f(p_{i})\left( A(p_{i} \right)^{e_{i}-1} \end{align*} $$ とし，$f(n)\lt n$ であることから，$n\gt 2$について，ある$k=k_{f}(n)$について， $$ f^{k}(n)=2 $$ であることから，$k_f(1)=k_f(2)=0$として $$ c_{f}(n)=\left\{ \begin{array}{ll} k_f(n) & n:\mbox{odd} \\ k_f(m)+1 & n:\mbox{even} \end{array} \right. $$ を定義し，先の$C(n)$と同様の関係式を有することを示しました．
　一方，宮田－山下は別視点で次のことを示しました．（2004.9 日本数学会秋季総合分科会・応用数学分科会）
　各素数$p$について，$f$ を$1\leq f(p)\lt p$であるような関数とし，$\varphi_{f}$を $$ \begin{align*} \varphi_{f}(n)=n\prod_{i=1}^{s}\dfrac{f(p_i)}{p_i} \qquad (n=\prod_{i=1}^{s}p_{i}^{e_{i}}) \end{align*} $$ と定め， $$ \begin{align*} L_{\varphi_{f}}(n)=\left\{ \begin{array}{ll} 0 & n=1 \\ L(\varphi_{f}(n))+\#\left|\{ p\in f^{-1}(1):p|n \}\right| & n\gt 1 \end{array} \right. \end{align*} $$ と定義すれば $$ \begin{align*} L_{\varphi_{f}}(xy)=L_{\varphi_{f}}(x)+L_{\varphi_{f}}(y) \end{align*} $$ が導かれます．
　証明の方針は，$x=\displaystyle\prod_{i=1}^{s}p_{i}^{e_{i}}$ の帰納法によります．$x$ 未満では成立しているものとしておきます．
$$ L_{\varphi_{f}}(x)=e_{1}L_{\varphi_{f}}(p_{1})+e_{2}L_{\varphi_{f}}(p_{2})+\cdots+e_{s}L_{\varphi_{f}}(p_{s})=\sum_{i=1}^{s}e_{i}L_{\varphi_{f}}(p_{i}) $$ を示せば十分です．
　$\alpha=\#|\{ p\in f^{-1}(1) : p|x \}$ として，素数 $p$ に対して，$f(p)=1$ なら $L_{\varphi_{f}}(f(p))=0$，そうでなければ $L_{\varphi_{f}}(f(p))=L_{\varphi_{f}}(p)$ であることに注意して $$ \begin{align*} L_{\varphi_{f}}(x)&=L_{\varphi_{f}}(\varphi(x))+\alpha \\ &=\sum_{i=1}^{s}(e_{i}-1)L_{\varphi_{f}}(p_{i})+\sum_{i=1}^{s}L_{\varphi_{f}}(f(p_{i}))+\alpha \\ &=\sum_{i=1}^{s}(e_{i}-1)L_{\varphi_{f}}(p_{i})+\sum_{i=1}^{s}L_{\varphi_{f}}(p_{i})-\alpha+\alpha \\ &=\sum_{i=1}^{s}e_{i}L_{\varphi_{f}}(p_{i}) \end{align*} $$ 　ここでの $\alpha=0,1$ が $L(x)$ での $x$ の扱い，奇偶の扱いに対応していて，$L(x)$ に関する対数関係式の別証を与えています．

　4.6. オイラー関数を拡張してみよう

　$1\lt n=\displaystyle\prod_{i=1}^{r}p_{i}^{e_{i}}$としておきます．
　

　4.7. $L(n)$について

　

　4.7.1. $L(x)=n$の集合$M(n)$

　$M(n)=\{~x\in \mathbb{N}~|~L(x)=n~\}$，$m(n)=|M(n)|,~m(0)=1$ とし，この$m(n)$を求めよう．$x=\displaystyle\prod p_i^{e_i}$の素因数分解について，$L(x)=\sum e_iL(p_i)$であることから，$m(n)$を求めることは，$L(x)=n$の$n$を$L(p_i)$を基にした分割数問題となります．したがって， $$ M_p(n)=\{~x:\mbox{prime}~|~L(x)=n~\}，\qquad c_n=\#|M_p(n)| $$ としたとき，Eulerによる無限和と無限積の恒等式を真似れば次の恒等式が得られます． $$ \begin{align*} \sum_{k=0}^{\infty}m(k)x^k &= \prod_{p}\frac{1}{1-x^{L(p)}}\\ &= \prod_{k=1}^{\infty} \prod_{i=1}^{c_k}\frac{1}{1-x^k}\\ &= \prod_{k=1}^{\infty} \frac{1}{(1-x^k)^{c_k}} \end{align*} $$ $c_n$が具体的に求められれば，$m(n)$が求められます．
$m(n)$までを求めたければ $$ \prod_{k=1}^{n}\displaystyle\frac{1}{~(1-x^{k})^{c_k}}~ $$ の計算でよいですね．
　OEIS(A064674):Number of primes q such that phiter(q)=n where phiter(n)=A064415(n), OEIS(A064416):Number of integers q such that phiter(q)=n where phiter(n) = A064415(n)では $n\leqq 16$ までなので，$n \leqq 23$ での $c_n,~m_n$ の計算結果（by Java）を以下に示しておきましょう． $c_n$ $m(n)$ について
$$ \begin{array}{ccc} n & c_n & m(n) \\ 1 & 2 & 2 \\ 2 & 2 & 5\\ 3 & 3 & 11\\ 4 & 6 & 26\\ 5 & 12 & 59\\ 6 & 23 & 137\\ 7 & 46 & 312\\ 8 & 94 & 719\\ 9 & 198 & 1651\\ 10 & 424 & 3816\\ 11 & 854 & 8757\\ 12 & 1859 & 20202\\ 13 & 3884 & 46440\\ 14 & 8362 & 106957\\ 15 & 17837 & 245989\\ 16 & 38977 & 566561\\ 17 & 84188 & 1303968\\ 18 & 183167 & 3002247\\ 19 & 398685 & 6910122 \\ 20 & 874078 & 15909143 \\ 21 & 1914563 & 36621627 \\ 22 & 4208672 & 84308428 \\ 23 & 9268875 & 194080801 \end{array} $$ 　以下，$M_p(9)$までの素数リストを示しておきましょう．
$M_p(1)=\{~2,~3~\}$
$M_p(2)=\{~5,~7~\}$
$M_p(3)=\{~11,~13,~19~\}$
$M_p(4)=\{~17,~23,29,~31,~37,~43~\}$
$M_p(5)=\{~41,~47,~53,~59,~61,~67,~71,~73,~79,~109,~127,163~\}$
$M_p(6)=\{~83,89,97,101,103,107,113,131,139,149,151,157,173,181,191,197,199,211,223,229,271,379,487\}$
$M_p(7)=\{137,167,179,193,227,233,239,241,251,263,269,277,281,283,293,307,311,313,317,331,337,347,$
$\qquad\qquad 349,367,373,383,397,419,421,431,433,439,457,463,491,509,523,541,547,571,631,653,757,811,$
$\qquad\qquad 883,1459 \}$
$M_p(8)=\{257,353,359,389,401,409,443,449,461,467,479,499,503,521,557,563,569,577,587,593,599,601,$
$\qquad\qquad 607,613,617,619,643,647,659,661,673,677,683,691,701,709,727,733,739,743,751,761,787,797,$
$\qquad\qquad 827,829,839,859,859,863,877,907,911,919,937,947,967,983,991,1009,1019,1033,1039,1051,1063,$
$\qquad\qquad 1087,1091,1093,1103,1117,1171,1279,1291,1297,1303,1307,1373,1423,1471,1483,1549,1567,1597,$
$\qquad \qquad 1621,1627,1783,1949,1999,2053,2269,2287,2647,2917,3079~\}$
$M_p(9)=\{~641,719,769,773,809,821,823,857,881,887,929,941,953,971,977,997,1013,1021,1031,1049,1061,$
$\qquad \qquad 1069,1109,1123,1129,1151,1153,1163,1181,1187,1193,1201,1213,1217,1223,1229,1231,1237,1249,$
$\qquad \qquad 1259,1277,1289,1301,1319,1321,1327,1367,1381,1399,1427,1429,1447,1451,1453,1481,1487,1489,$
$\qquad \qquad 1493,1499,1511,1523,1531,1559,1671,1579,1583,1597,1609,1613,1657,1663,1667,1669,1693,1699,$
$\qquad \qquad 1709,1721,1723,1733,1741,1747,1753,1759,1777,1787,1789,1801,1811,1823,1831,1847,1861,1867,$
$\qquad \qquad 1873,1877,1879,1901,1933,1851,1979,1987,2003,2011,2017,2019,2039,2083,2087,2089,2111,2129,$
$\qquad \qquad 2131,2143,2161,2179,2203,2207,2213,2221,2237,2239,2243,2251,2281,2293,2311,2341,2357,2371,$
$\qquad \qquad 2377,2383,2389,2399,2423,2437,2503,2521,2539,2549,2557,2591,2593,2609,2617,2677,2683,2699,$
$\qquad \qquad 2711,2719,2731,2749,2791,2843,2851,2887,2927,2971,3011,3049,3067,3109,3187,3253,3259,3271,$
$\qquad \qquad 3307,3319,3331,3511,3529,3533,3547,3557,3583,3613,3727,3823,3889,3907,3919,3943,4051,4159,$
$\qquad \qquad 4219,4447,4549,4663,4789,4861,4871,4903,5023,5347,5419,5869,6823,6967,8803~\}$

　4.7.2. $M_p(n)$の要素について

　また，$M_p(n)$の要素$q$については $$ \max_{q\in M_p(n)} q \leqq 2\cdot3^{n-1}+1$$ が成立しているが，この不等式での等号は外せません．$2\cdot 3^{n-1}+1$が素数になる場合があるからです．ただし，$n\longrightarrow \infty$では，（実験では）素数になる確率は下がってゆくような振舞いを見せています．
　因みに$n<5000$の範囲で$y(n)=2\cdot 3^{n-1}+1$が素数となるのは$n=1,2,3,5,6,7,10,17,18,31,55,58,61,66,133,181,321, 697, 783, 823, 898, 1253, 1455, 4218~$の24個だけです（by Maple \& Python）
． $$ \begin{align} y(181) &= ~1523546~9609173278~4678579455 \notag \\ & ~4412311235~0084960280~4790393448 \notag \\ & ~0031314899 ~1427468606~6076039203 \notag \end{align} $$ 　 　この型の数については，既に，OIESでは100万ほどまで調べられています．(A003306:Numbers $n$ such that $2*3^n+1$ is prime)
　そこでは，
　$0, 1, 2, 4, 5, 6, 9, 16, 17, 30, 54, 57, 60, 65, 132, 180, 320,696, 782, 822,$
　$897, 1252, 1454, 4217, 5480, 6225, 7842,12096, 13782, 17720,$
　$43956, 64822, 82780, 105106, 152529,165896, 191814, 529680, 1074726, 1086112, 1175232$
の41個と報告されています．ここでの記法では，これらの数に$+1$したものとなります．無限に存在するでしょうが，分布のorderについては，未解明です．

　4.7.3. $\displaystyle\sum \dfrac{1}{\varphi^s}$

　$\displaystyle\sum_{n=1}^{\infty}\frac{1}{~\varphi(n)^s~}$なる関数を考えてみ ましょう．
　具体的に計算してみると，この級数は $$ \begin{align} \frac{1}{1^s}&+\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{2^s}+\frac{1}{6^s}+\frac{1}{4^s}+\frac{1}{6^s} \notag \\ & +\frac{1}{4^s} +\frac{1}{10^s}+\frac{1}{4^s}+\cdots \notag \\ &=\sum_{n=1}^{\infty}\frac{h(n)}{n^s} \notag \end{align} $$ であり，ディリクレ級数の特別な場合(?)となります．しかも，この係数$h(n)$は次のような数となっています． $$ H(n)=\{~ x~|~\varphi(x)=n ~\},\qquad h(n)=\#|H(n)| $$ 　因みに，$n\geqq 3$なる奇数$n$については$h(n)=0$は自明ですが，$p\gt 3$なる素数$p$について，$2p+1$が素数でない場合にも$h(2p)=0$です．
　　いま，$\varphi$で考えましたたが，この$\varphi$を数論的関数$g(n)$（ただし，$g(n)\geqq 1$かつ$H(n)=\{~ x~|~g(x)=n ~\},\qquad h(n)=|H(n)|\lt \infty$）で置き換えてもディリクレ級数の特別な場合となります．
　また$L$についてのディリクレ級数 $$ \sum_{n=1}^{\infty}\frac{~L(n)~}{n^s} $$ は，$L(x)$に関する評価不等式から，実数$s$で $$ \sum_{n=1}^{\infty}\frac{~L(n)~}{n^s} \lt \zeta'(s) $$ ．

　4.8. ジョルダンのトーシェント関数

　オイラー関数の一つの拡張として，ジョルダンの標準形やJordan-Hölder-Schreierの定理等で知られるジョルダン(Camille Jordan)の仕事に因んで命名されているジョルダンのトーシェント関数(Jordan's totient function)があります．ジョルダンの仕事とは，"Mémoire sur les équations différentielles linéaires à intégrale algéebrique"(J. Reine Angew. Math. 84 (1878), 89–215)の中で $$ \#|{\rm GL}(n,\mathbf Z/n\mathbf Z)|=n^{\frac{m(m-1)}{2}}\prod_{k=1}^{m}J_{k}(n) $$ を示したことによります．
　$n$以下の自然数から$m$個を重複を許して選び，その$m$個と$n$の最大公約数が$(k,n)=1$ となるようなもの$k$の総数を$J_{m}(n)$で表していることになります． $$ \begin{align*} J_{k}(n)=n^{k}\prod_{p|n}\left( 1-\frac{1}{~p^k~}\right) \end{align*} $$ (ディリクレ)合成積の表現をすれば $$ \begin{align*} J_{k}=\mu\ast \iota_{k} \end{align*} $$

---

***

???